What is the Standard Error of Measurement (SEM)?
The Standard Error of Measurement (SEM) indicates the amount of error around the observed score. The observed score, the score we retrieve, store and analyse from an OSCE, is in fact the result of the true score and error around this true score. If we want a reliable decision around passing or failing a station e.g. an OSCE, we need to incorporate the SEM in that decision.
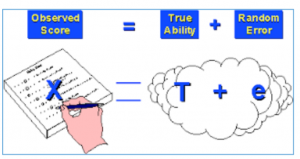
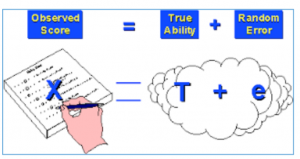
Observed Score is the true ability (true score) of the student plus the random error around that true score. The error is associated with the reliability or internal consistency of score sheets used in OSCEs. Within our system, Qpercom calculates Cronbach’s alpha as a reliability score indicating how consistent scores are being measured, and the Intra Class Correlation coefficient; how reliable are scores between the different stations (Silva et al., 2017). These classical psychometric measures of the data can be used to calculate the SEM. An observed score +/- the SEM means that with 68% certainty the ‘true score’ of that station is somewhere in between the actual score, plus or minus the SEM. In principle, one should consider plus or minus the 95% Confidence Interval, which is the Observed score plus or minus 1.96 * SEM (Zimmerman & Williams, 1966).

Incorporating qualitative scores in the judgment of student performance is becoming more established practice in assessment of medical & healthcare observational assessment. The simplest way of addressing borderline scores is known as BGA, Borderline Group Average. The average scores of students assessed on a Global Rating Score as borderline by their assessors, on a Global Rating Score is simple and reliable, if a large amount of students are marked this way. With small numbers this method is considered unreliable. Borderline Regression Method incorporates the actual item total score from the score-sheet, and the professional opinion of the examiner expressed on the Global Rating Score (GRS). Similar to the BGA, the GRS is a qualitative score varying from Fail, Borderline, Pass, Good and Excellent (Method 1) where the cut-score is associated with borderline performance of the student, according to the examiner’s professional opinion.
As a result, the cut-score is estimated between Fail and Pass scores. In addition to method 1, in method 2, Fail, Borderline Fail and Borderline Pass, Good Pass and Excellent is added to the scale. In the latter case the cut-score is estimated between Borderline Fail and Borderline Pass, which compared to method 1 is higher. Using the BRM, a forecast regression method is used with the observed raw score (y-axis) and the GRS (x-axis) where ‘intercept’ and ‘slope’ determines the direction of the regression line. Where the vertical line associated with the qualification Borderline on the X-axis crosses the Y-axis, and the horizontal line from this point towards the Y-axis represent the ‘new/adjusted cut-score’. This method is known as retrospective standard setting. Angoff, Cohen and others are forms of prospective standard setting, taking into account the exam creator’s perception of the ability of students to pass the exam. Using retrospective standard setting considers not only the ability of students, but also the difficulty of the examination.
Both methods either use the raw observed score or the raw adjusted score. The last one uses a different/adjusted cut-score, but for both methods the SEM needs to be incorporated. As the SEM represents the error around the observed score, in case of the first BMI (Body Mass Index) station, the student with an observed score of 60% actually had a score somewhere between 54.3% and 65.7% (with 68% CI). If we want to be 95% sure about their true ability the score is estimated to be between 60% – 11.20 = 48.80 and 60% + 11.20 is 71.20. This is the case if Cronbach’s alpha is used as a matter of internal consistency. How consistent are the items used in a score sheet and in determining ‘good’ and ‘bad’ performing students.
Cronbach’s alpha depends on numbers (n), the higher n, the number of students going through the exam the more reliable alpha is. However, using BRM, the SEM differs depending on the extremes of the GBR scores. Whereas, using Cronbach’s alpha, the adjustment of scores is a linear approach independent of scores as such.

In Ireland the cut-score is 50% for each of the stations, not considering error due to examiners variability and item variability e.g. the reliability of the station. In this particular case, taking the error and 95% CI into account, anyone with a score of < 61.20 should get a fail (McManus, 2012)!
There are some illustrative YouTube videos available explaining the meaning of the SEM and how to calculate the SEM in Excel. We in Qpercom are working to make SEM available online in our systems to assist in educational decision-making. Literature provides contradictory insights, however the SEM calculated using Cronbach’s alpha could also be used for BRM. We work with an in between solution, whereas the SEM for extreme scores (the higher and lower 10% of scores) should be calculated differently. Qpercom Observe will soon be equipped with our final chosen approach.
References
McManus, I. C. (2012). The misinterpretation of the standard error of measurement in medical education: a primer on the problems, pitfalls and peculiarities of the three different standard errors of measurement. Med Teach, 34(7), 569-576. doi:10.3109/0142159X.2012.670318
Silva, A. G., Cerqueira, M., Raquel Santos, A., Ferreira, C., Alvarelhao, J., & Queiros, A. (2017). Interrater reliability, standard error of measurement and minimal detectable change of the 12- item WHODAS 2.0 and four performance tests in institutionalized ambulatory older adults. Disabil Rehabil, 1-8. doi:10.1080/09638288.2017.1393112
Zimmerman, D. W., & Williams, R. H. (1966). Interpretation of the standard error of measurement when true scores and error scores on mental tests are not independent. Psychol Rep, 19(2), 611-617. doi:10.2466/pr0.1966.19.2.611





























